6.3 KiB
Binary Logistic Regression
Binary logistic regression are used to predict an binary issue (win/loss, true/false) according to various parameters. First, we have to choose a polynomial function $h_w(x)$ according to the data complexity (see \textit{data/binary\_logistic.csv}). In our case, we want to predict our issue (1 or 0) according to two parameters. Thus:
\begin{equation} h_w(x_1,x_2) = w_1 + w_2x_1 + w_3x_2 \end{equation}However, the function we are looking for should return a binary result! To achieve this goal, we can use a sigmoid (or logistic) with the following property $\mathbb{R} \to ]0;1[$ with the following form:
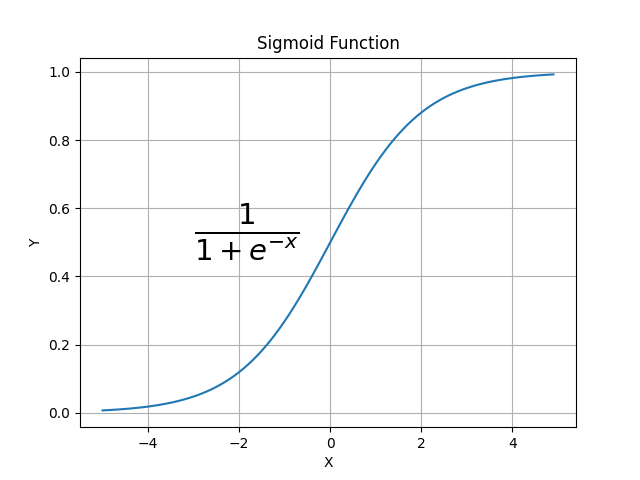
To this end, we can define the following function: \begin{equation}\label{eq:cost} g_w(x_1,x_2) = \frac{1}{1+e-h_w(x_1,x_2)}
\end{equation}
The next step is to define a cost function. A common approach in binary logistic function is to use the Cross-Entropy loss function. It is much more convenient than the classical Mean Square Error used in polynomial regression. Indeed, the gradient is stronger even for small error (see here for more informations). Thus, it looks like the following: \begin{equation}\label{eq:cost} J(w) = -\frac{1}{n} ∑i=0^n ≤ft[y(i)log(g_w(x_1(i),x_2(i))) + (1-y(i))log(1-g_w(x_1(i),x_2(i)))\right]
\end{equation}
With $n$ the number of observations, $x_j^{(i)}$ is the value of the $j^{th}$ independant variable associated with the observation $y^{(i)}$. The next step is to $min_w J(w)$ for each weight $w_i$ (performing the gradient decent, see here). Thus we compute each partial derivatives:
\begin{align*} \frac{\partial J(w)}{\partial w_1}&=\frac{\partial J(w)}{\partial g_w(x_1,x_2)}\frac{\partial g_w(x_1,x_2)}{\partial h_w(x_1,x_2)}\frac{\partial h_w(x_1,x_2)}{\partial w_1}\nonumber\\ \frac{\partial J(w)}{\partial g_w(x_1,x_2)}&=-\frac{1}{n} \sum_{i=0}^n \left[y^{(i)}\frac{1}{g_w(x_1^{(i)},x_2^{(i)})} + (1-y^{(i)})\times\frac{1}{1-g_w(x_1^{(i)},x_2^{(i)})}\times (-1)\right]\nonumber\\ &=-\frac{1}{n} \sum_{i=0}^n \left[\frac{y^{(i)}}{g_w(x_1^{(i)},x_2^{(i)})} - \frac{1-y^{(i)}}{1-g_w(x_1^{(i)},x_2^{(i)})}\right]\nonumber\\ &=-\frac{1}{n} \sum_{i=0}^n \left[\frac{y^{(i)}(1-g_w(x_1^{(i)},x_2^{(i)}))}{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))} - \frac{g_w(x_1^{(i)},x_2^{(i)})(1-y^{(i)})}{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))}\right]\nonumber\\ &=-\frac{1}{n} \sum_{i=0}^n \left[\frac{y^{(i)}\cancel{-y^{(i)}g_w(x_1^{(i)},x_2^{(i)})} -g_w(x_1^{(i)},x_2^{(i)})\cancel{+y^{(i)}g_w(x_1^{(i)},x_2^{(i)})}}{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))}\right]\nonumber\\ &=\frac{1}{n} \sum_{i=0}^n \left[\frac{-y^{(i)} +g_w(x_1^{(i)},x_2^{(i)})}{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))}\right]\nonumber\\ \frac{\partial g_w(x_1,x_2)}{\partial h_w(x_1,x_2)}&=\frac{\partial (1+e^{-h_w(x_1,x_2)})^{-1}}{\partial h_w(x_1,x_2)}=-(1+e^{-h_w(x_1,x_2)})^{-2}\times \frac{\partial (1+e^{-h_w(x_1,x_2)})}{\partial h_w(x_1,x_2)}\nonumber\\ &=-(1+e^{-h_w(x_1,x_2)})^{-2}\times -e^{-h_w(x_1,x_2)}=\frac{e^{-h_w(x_1,x_2)}}{(1+e^{-h_w(x_1,x_2)})^2}\nonumber\\ &=\frac{e^{-h_w(x_1,x_2)}}{(1+e^{-h_w(x_1,x_2)})(1+e^{-h_w(x_1,x_2)})}=\frac{1}{(1+e^{-h_w(x_1,x_2)})}\frac{e^{-h_w(x_1,x_2)}}{(1+e^{-h_w(x_1,x_2)})}\nonumber\\ &=\frac{1}{(1+e^{-h_w(x_1,x_2)})}\frac{e^{-h_w(x_1,x_2)}+1-1}{(1+e^{-h_w(x_1,x_2)})}=\frac{1}{(1+e^{-h_w(x_1,x_2)})}\left(1+\frac{-1}{(1+e^{-h_w(x_1,x_2)})}\right)\nonumber\\ &=g_w(x_1,x_2)(1-g_w(x_1,x_2))\nonumber\\ \frac{\partial h_w(x_1,x_2)}{\partial w_1}=1\nonumber\\ \text{Finally:}\\ \frac{\partial J(w)}{\partial w_1}&=\frac{1}{n} \sum_{i=0}^n \left[\frac{-y^{(i)}+g_w(x_1^{(i)},x_2^{(i)})}{\cancel{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))}} \times \cancel{g_w(x_1^{(i)},x_2^{(i)})(1-g_w(x_1^{(i)},x_2^{(i)}))} \right]\nonumber\\ &=\frac{1}{n} \sum_{i=0}^n \left[-y^{(i)}+g_w(x_1^{(i)},x_2^{(i)})\right] \end{align*} \begin{align*} \text{Similarly:}\\ \frac{\partial J(w)}{\partial w_2}&=\frac{1}{n} \sum_{i=0}^n x_1\left[-y^{(i)}+g_w(x_1^{(i)},x_2^{(i)})\right]\\ \frac{\partial J(w)}{\partial w_1}&=\frac{1}{n} \sum_{i=0}^n x_2\left[-y^{(i)}+g_w(x_1^{(i)},x_2^{(i)})\right]\\ \end{align*}For more informations on binary logistic regression, here are usefull links:
Desision Boundary
The method used here is similar to the one used here. In binary logistic regression, decision boundary is located where:\\ \[g_w(x_1,x_2)=0.5 \implies h_w(x_1,x_2)=0\] In addition we now that our decision boundary has the following form \[x_2=ax_1+b\] Thus, we can easily deduce b since if $x_1=0$ we have $x_2=a\times 0 + b \implies x_2=b$. Thus:
\begin{equation} h_w(0,x_2)=w_1 + w_3x_2=0\\ \implies x_2=\frac{-w_1}{w_3} \end{equation}To deduce the a coefficient, it is slighly more complicated. If we know two points $(x_1^a,x_2^a)$ and $(x_1^b,x_2^b)$ on the decision boundary line, we know that $a=\frac{x_2^b-x_2^a}{x_1^b-x_1^a}$. thus if we compute:
\begin{align*} h_w(X_1^b,x_2^b)-h_w(X_1^a,x_2^a)&=\cancel{w_1}+w_2x_1^b+w_3x_2^b\cancel{-w_1}-w_2x_1^a-w_3x_2^a = 0 \\ &\implies w_2(x_1^b-x_1^a)+w_3(x_2^b-x_2^a) = 0 \implies \frac{w_2}{-w_3}=\frac{(x_1^b-x_1^a)}{(x_2^b-x_2^a)}=a \end{align*}Thus we have the decision boundary defined as follow: \[ d(x) = \frac{w_2}{-w_3} x - \frac{w_1}{w_3} \]